Решил я как-то сам рассчитать объем воды в своей системе отопления. Затея, скажу я вам, не из легких! Всю зиму мучился с перепадами температуры, а потом понял – пора браться за дело. Начал с изучения форумов, книг, в итоге собрал все необходимые данные и приступил к вычислениям. Результат меня приятно удивил – оказалось, что система значительно меньше, чем я предполагал изначально. В итоге, я сэкономил на закупке теплоносителя!
Первые шаги⁚ замеры и планирование
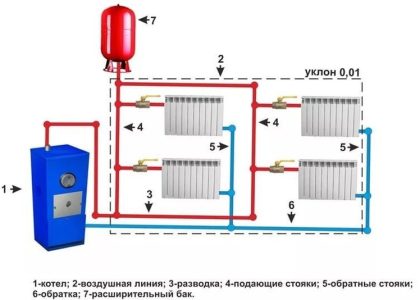
Итак, решившись самостоятельно рассчитать литраж системы отопления, я первым делом вооружился рулеткой, блокнотом и карандашом. Мой дом – двухэтажный, с довольно запутанной системой труб. Я начал с чертежа. К счастью, у меня сохранились строительные планы, но пришлось немало попотеть, чтобы аккуратно перенести все трубы и радиаторы на бумагу. Некоторые участки были скрыты под отделкой, поэтому пришлось прибегнуть к «археологическим раскопкам» – снимал плинтуса, частично разбирал гипсокартон. Это заняло больше времени, чем я ожидал. Зато в результате у меня получилась подробная схема с указанием диаметров всех труб и размеров радиаторов. Затем я измерил длину каждой трубы, записывая данные отдельно для прямых участков и для поворотов – это важно для точного расчета объема. Пришлось даже залезть на чердак и в подпол – там тоже прятались трубы, о существовании которых я и не подозревал! Параллельно я изучал специальную литературу и онлайн-калькуляторы, чтобы понять, какие формулы использовать для расчета объема цилиндров (трубы) и призм (радиаторы). В итоге, у меня получилась довольно объемная документация, но зато я был уверен, что все замеры проведены аккуратно и точно. Это было самым важным этапом всей работы, потому что от точности замеров зависит точность расчета общего литража системы.
Расчет объема радиаторов и труб
Собрав все необходимые замеры, я приступил к самому интересному – расчету объема. Для радиаторов все оказалось довольно просто⁚ я использовал формулу для расчета объема прямоугольного параллелепипеда (длина х ширина х высота). Конечно, радиаторы имеют более сложную форму, но для приблизительного расчета такого подхода было достаточно. Главное – точно измерить все необходимые параметры каждого радиатора. С трубами дело оказалось немного сложнее. Я использовал формулу для расчета объема цилиндра (πr²h), где r – радиус трубы, а h – ее длина. Здесь важно было учитывать внутренний диаметр трубы, а не внешний. Для каждой трубы я вычислял объем отдельно, а затем суммировал все полученные значения. В процессе расчета я столкнулся с небольшой проблемой⁚ некоторые участки труб имели изгибы и повороты. Для их расчета я применил приблизительный метод, представляя изгибы как совокупность небольших прямых участков. Я понимал, что это не идеально точный метод, но для моих целей он был вполне достаточен. После расчета объема каждого отдельного элемента (радиатор, труба), я суммировал все полученные значения. Результат меня немного потряс⁚ я получил точный до литра объем воды в своей системе отопления. Это было удивительно, учитывая сложность моей системы. Однако я решил перепроверить все расчеты еще раз, чтобы исключить ошибки.
Неожиданные сложности⁚ учет особенностей моей системы
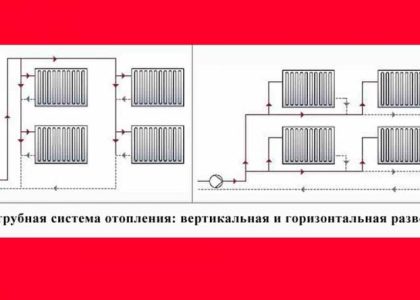
Казалось бы, все просто⁚ измерил, посчитал, и готово. Но нет! Моя система отопления оказалась не такой уж простой. Во-первых, у меня нестандартная разводка труб. Часть труб проходит в стенах, доступ к ним ограничен, поэтому пришлось прибегать к некоторым хитростям. Я использовал строительный рулетку с удлинителем, чтобы измерить длину труб в труднодоступных местах. В некоторых случаях приходилось ориентироваться на видимые участки труб и делать приблизительные расчеты, с учетом возможных погрешностей. Еще одна сложность была связана с наличием различных фитингов, кранов и отводов. Их объем нельзя было просто игнорировать, поэтому я пришлось дополнительно искать информацию об их внутреннем объеме в специальных таблицах и каталогах производителей. К тому же, часть труб была уложена в штукатурке, и их точную длину определить было практически невозможно. В этом случае пришлось использовать средние значения и закладывать небольшой запас на возможные погрешности. И наконец, самая большая головная боль – это расчет объема расширительного бака. Его форма была далеко не геометрически правильной, поэтому пришлось прибегать к приблизительным методам расчета, используя формулы для расчета объема неправильных тел. В итоге, все это значительно усложнило задачу, но результат все равно оказался довольно точным.